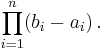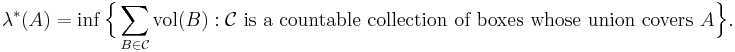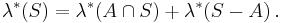Lebesgue measure

In measure theory, the Lebesgue measure, named after Henri Lebesgue, is the standard way of assigning a length, area or volume to subsets of Euclidean space. It is used throughout real analysis, in particular to define Lebesgue integration. Sets which can be assigned a volume are called Lebesgue measurable; the volume or measure of the Lebesgue measurable set A is denoted by λ(A). Lebesgue measures of infinite sets are possible, but even so, assuming the axiom of choice, not all subsets of Rⁿ are Lebesgue measurable. The "strange" behavior of non-measurable sets gives rise to such statements as the Banach–Tarski paradox, a consequence of the axiom of choice.

Henri Lebesgue described this measure in the year 1901, followed the next year by his description of the Lebesgue integral. Both were published as part of his dissertation in 1902.^[1]

Lebesgue measure is often denoted 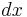$\,dx$ , but this should not be confused with the distinct notion of a volume form.

1 Examples
2 Properties
3 Null sets
4 Construction of the Lebesgue measure
5 Relation to other measures
6 See also
7 References

Examples

Any closed interval [a, b] of real numbers is Lebesgue measurable, and its Lebesgue measure is the length b−a. The open interval (a, b) has the same measure, since the difference between the two sets consists only of the end points a and b and has measure zero.
Any Cartesian product of intervals [a, b] and [c, d] is Lebesgue measurable, and its Lebesgue measure is (b−a)(d−c), the area of the corresponding rectangle.
The Cantor set is an example of an uncountable set that has Lebesgue measure zero.
Vitali sets are examples of sets that are not measurable with respect to the Lebesgue measure. Their existence relies on the axiom of choice. In 1970, Robert M. Solovay showed that the existence of sets that are not Lebesgue measurable is not provable within the framework of Zermelo–Fraenkel set theory in the absence of the axiom of choice.^[2]

Properties

The Lebesgue measure on Rⁿ has the following properties:

If A is a cartesian product of intervals I₁ × I₂ × ... × I_n, then A is Lebesgue measurable and $\lambda (A)=|I_1|\cdot |I_2|\cdots |I_n|.$ Here, |I| denotes the length of the interval I.
If A is a disjoint union of countably many disjoint Lebesgue measurable sets, then A is itself Lebesgue measurable and λ(A) is equal to the sum (or infinite series) of the measures of the involved measurable sets.
If A is Lebesgue measurable, then so is its complement.
λ(A) ≥ 0 for every Lebesgue measurable set A.
If A and B are Lebesgue measurable and A is a subset of B, then λ(A) ≤ λ(B). (A consequence of 2, 3 and 4.)
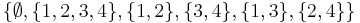Countable unions and intersections of Lebesgue measurable sets are Lebesgue measurable. (Not a consequence of 2 and 3, because a family of sets that is closed under complements and disjoint countable unions need not be closed under countable unions: $\{\emptyset, \{1,2,3,4\}, \{1,2\}, \{3,4\}, \{1,3\}, \{2,4\}\}$ .)
If A is an open or closed subset of Rⁿ (or even Borel set, see metric space), then A is Lebesgue measurable.
If A is a Lebesgue measurable set, then it is "approximately open" and "approximately closed" in the sense of Lebesgue measure (see the regularity theorem for Lebesgue measure).
Lebesgue measure is both locally finite and inner regular, and so it is a Radon measure.
Lebesgue measure is strictly positive on non-empty open sets, and so its support is the whole of Rⁿ.
If A is a Lebesgue measurable set with λ(A) = 0 (a null set), then every subset of A is also a null set. A fortiori, every subset of A is measurable.
If A is Lebesgue measurable and x is an element of Rⁿ, then the translation of A by x, defined by A + x = {a + x : a ∈ A}, is also Lebesgue measurable and has the same measure as A.
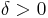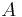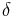If A is Lebesgue measurable and $\delta>0$ , then the dilation of $A$ by $\delta$ defined by 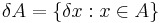$\delta A=\{\delta x:x\in A\}$ is also Lebesgue measurable and has measure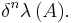 $\delta^{n}\lambda\,(A).$
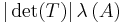More generally, if T is a linear transformation and A is a measurable subset of Rⁿ, then T(A) is also Lebesgue measurable and has the measure $|\det(T)|\, \lambda\,(A)$ .

All the above may be succinctly summarized as follows:

The Lebesgue measurable sets form a σ-algebra containing all products of intervals, and λ is the unique complete translation-invariant measure on that σ-algebra with $\lambda([0,1]\times [0, 1]\times \cdots \times [0, 1])=1.$

The Lebesgue measure also has the property of being σ-finite.

Null sets

A subset of Rⁿ is a null set if, for every ε > 0, it can be covered with countably many products of n intervals whose total volume is at most ε. All countable sets are null sets.

If a subset of Rⁿ has Hausdorff dimension less than n then it is a null set with respect to n-dimensional Lebesgue measure. Here Hausdorff dimension is relative to the Euclidean metric on Rⁿ (or any metric Lipschitz equivalent to it). On the other hand a set may have topological dimension less than n and have positive n-dimensional Lebesgue measure. An example of this is the Smith–Volterra–Cantor set which has topological dimension 0 yet has positive 1-dimensional Lebesgue measure.

In order to show that a given set A is Lebesgue measurable, one usually tries to find a "nicer" set B which differs from A only by a null set (in the sense that the symmetric difference (A 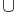− B) $\cup$ (B − A) is a null set) and then show that B can be generated using countable unions and intersections from open or closed sets.

Construction of the Lebesgue measure

The modern construction of the Lebesgue measure is an application of Carathéodory's extension theorem. It proceeds as follows.

Fix n ∈ N. A box in Rⁿ is a set of the form

$B=\prod_{i=1}^n [a_i,b_i] \, ,$

where b_i ≥ a_i. The volume vol(B) of this box is defined to be

$\prod_{i=1}^n (b_i-a_i) \, .$

For any subset A of Rⁿ, we can define its outer measure λ*(A) by:

$\lambda^*(A) = \inf \Bigl\{\sum_{B\in \mathcal{C}}\operatorname{vol}(B)�: \mathcal{C}\text{ is a countable collection of boxes whose union covers }A\Bigr\} .$

We then define the set A to be Lebesgue measurable if for every S in Rⁿ,

$\lambda^*(S) = \lambda^*(A \cap S) + \lambda^*(S - A) \, .$

These Lebesgue measurable sets form a σ-algebra, and the Lebesgue measure is defined by λ(A) = λ*(A) for any Lebesgue measurable set A.

According to the Vitali theorem there exists a subset of the real numbers R that is not Lebesgue measurable. Much more is true: if A is any subset of 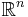$\R^n$ of positive measure, then A has subsets which are not Lebesgue measurable.

Relation to other measures

The Borel measure agrees with the Lebesgue measure on those sets for which it is defined; however, there are many more Lebesgue-measurable sets than there are Borel measurable sets. The Borel measure is translation-invariant, but not complete.

The Haar measure can be defined on any locally compact group and is a generalization of the Lebesgue measure (Rⁿ with addition is a locally compact group).

The Hausdorff measure is a generalization of the Lebesgue measure that is useful for measuring the subsets of Rⁿ of lower dimensions than n, like submanifolds, for example, surfaces or curves in R³ and fractal sets. The Hausdorff measure is not to be confused with the notion of Hausdorff dimension.

It can be shown that there is no infinite-dimensional analogue of Lebesgue measure.

References

↑ Henri Lebesgue (1902). Intégrale, longueur, aire. Université de Paris.
↑ Solovay, Robert M. (1970). "A model of set-theory in which every set of reals is Lebesgue measurable". Annals of Mathematics. Second Series 92 (1): 1–56. doi:10.2307/1970696.